Title: Free Fall and Air Resistance
Name: Ray Arellano
Lab Partners: David Hwang & Jesus Hernandez
Date: 3/13/17
This lab involved modeling the effects of air resistance on an object experiencing free fall. It is believed that the effects of air resistance vary depending on the mass of the object falling, the material of the object, and the shape of the object.
In this lab, paper coffee filters were the objects that were put into free fall. Our job was to measure the terminal velocity of coffee filters as they descended from a certain height. When the force the object has while descending matches the force of air resistance, the object no longer accelerates and travels with a constant velocity known as its terminal velocity. This terminal velocity should vary as we changed the mass of the object descending by stacking coffee filters, adding one more than was present during the previous trial.
This image shows how the filter was dropped from a balcony. We used the Video Capture feature on the laptop that was provided in order to record the path of the coffee filters. Using Video Capture allowed us to see how far the coffee filters traveled at a specific time. Taking this information gave us the relationship between distance and time, resulting in information about the object's velocity. Eventually, we developed a graph that identified the air resistance force for the different masses we used in the experiment. Taking a power fit for this graph allowed us to derive our values for "k" and "n", which we used in the model Fresistance = kv^n. Once we had these values, we placed them into the spreadsheet we made and found the terminal velocity for the coffee filters.
This image shows the format we were supposed to use in order to calculate the terminal velocity of the coffee filters. We used the appropriate values for "k" and "n" in this specific sheet (5 filters).
In this image, we see the terminal velocity of five coffee filters. After t= 2.30s, the velocity of the five coffee filters began to show trends of staying constant. That is, they had almost reached their terminal velocity. The terminal velocity was 2.871373 m/s.
This model for finding the terminal velocity of an object experiencing free fall and air resistance works. However, we initially took a power fit of the wrong graphs and got wrong values of "k" and "n" which did not allow us to find the terminal velocity of the coffee filters. After our instructor reminded us of the appropriate graph to take a power fit of, our group was able to create the spreadsheet we needed to find the terminal velocities.
Monday, March 20, 2017
Wednesday, March 15, 2017
3/6/17: Calculating the Density of a Cylinder
Title: Calculating the Density of a Cylinder
Name: Ray Arellano
Lab Partners: David Hwang & Jesus Hernandez
Date: 3/6/17
The purpose of this lab was to understand the topic of propagated uncertainty. In order to achieve this, students were supposed to take the measurements of a metallic cylinder and come up with a way to find its density.
Measurements can only be so precise, so a level of uncertainty remains for each measurement. Therefore, the density of the cylinder would also have a level of uncertainty to its value. A length-measuring instrument was used in order to calculate the height and diameter of the cylinder used. Our job was to use these measurements, assign a deviation for the measurements taken, develop an equation for the density of the cylinder, and use the partial derivative method of finding the propagated uncertainty of the cylinder. The partial derivative method calls for using our equation ⍴ (rho- density) and taking the partial derivative of this equation with respect to the variables m (mass), h (height), and d (diameter); we then multiply these partial derivatives by the deviation assigned to each measurement and square the resulting products, add them, and raise the sum to a power of 1/2. Students could also use the natural logarithm method for solving for the propagated uncertainty of the density of the cylinder.
This image shows the apparatus used in this experiment. Shown are a vernier caliper, which was used to measure the height and diameter of the cylinder, and two cylinders of which only one was used for this experiment. The vernier caliper has precise measurements, but our interpretation of those measurements depends on how well we can see the marks on the vernier caliper and our judgement when deciding to round up or down to the nearest marks.
Shown above are the calculations for the density of the cylinder we chose. The bottom, left corner displays the measurements for the mass, height, and diameter of the cylinder along with the deviation assigned to each one. The upper, right corner of the space with the calculations displays the equation for density. The center of the space with calculations shows the partial derivatives of the equation for density and these partial derivatives put into the equation for solving for the propagated uncertainty of a measurement or value. Lastly, we have our result for the density and the propagated uncertainty of the cylinder enclosed in a rectangular shape in the center of the white space.
People can assume that measurements are perfect. However, this is not true all of the time. Although we'd like to believe that measurements taken with tools and calculations are perfect, a degree of uncertainty is always present in the calculations/measurements.
Coming up with an answer was the part of this experiment that my partners and I had the most trouble with. We attempted to use both the partial derivative method and the natural logarithm method for solving for the propagated uncertainty of the the cylinder's density. Initially, our answers did not match and we were confused about which answer was the correct one. After several attempts we found that the result obtained using the natural logarithm method was the same as the partial derivative method. However, the calculation using the partial derivative method was a bit easier to follow so we chose to use this image to represent our calculations.
Name: Ray Arellano
Lab Partners: David Hwang & Jesus Hernandez
Date: 3/6/17
The purpose of this lab was to understand the topic of propagated uncertainty. In order to achieve this, students were supposed to take the measurements of a metallic cylinder and come up with a way to find its density.
Measurements can only be so precise, so a level of uncertainty remains for each measurement. Therefore, the density of the cylinder would also have a level of uncertainty to its value. A length-measuring instrument was used in order to calculate the height and diameter of the cylinder used. Our job was to use these measurements, assign a deviation for the measurements taken, develop an equation for the density of the cylinder, and use the partial derivative method of finding the propagated uncertainty of the cylinder. The partial derivative method calls for using our equation ⍴ (rho- density) and taking the partial derivative of this equation with respect to the variables m (mass), h (height), and d (diameter); we then multiply these partial derivatives by the deviation assigned to each measurement and square the resulting products, add them, and raise the sum to a power of 1/2. Students could also use the natural logarithm method for solving for the propagated uncertainty of the density of the cylinder.
This image shows the apparatus used in this experiment. Shown are a vernier caliper, which was used to measure the height and diameter of the cylinder, and two cylinders of which only one was used for this experiment. The vernier caliper has precise measurements, but our interpretation of those measurements depends on how well we can see the marks on the vernier caliper and our judgement when deciding to round up or down to the nearest marks.
Shown above are the calculations for the density of the cylinder we chose. The bottom, left corner displays the measurements for the mass, height, and diameter of the cylinder along with the deviation assigned to each one. The upper, right corner of the space with the calculations displays the equation for density. The center of the space with calculations shows the partial derivatives of the equation for density and these partial derivatives put into the equation for solving for the propagated uncertainty of a measurement or value. Lastly, we have our result for the density and the propagated uncertainty of the cylinder enclosed in a rectangular shape in the center of the white space.
People can assume that measurements are perfect. However, this is not true all of the time. Although we'd like to believe that measurements taken with tools and calculations are perfect, a degree of uncertainty is always present in the calculations/measurements.
Coming up with an answer was the part of this experiment that my partners and I had the most trouble with. We attempted to use both the partial derivative method and the natural logarithm method for solving for the propagated uncertainty of the the cylinder's density. Initially, our answers did not match and we were confused about which answer was the correct one. After several attempts we found that the result obtained using the natural logarithm method was the same as the partial derivative method. However, the calculation using the partial derivative method was a bit easier to follow so we chose to use this image to represent our calculations.
3/8/17: Finding the Stopping Distance of An Elephant
Title: Finding the Stopping Distance of An Elephant
Name: Ray Arellano
Lab Partners: David Hwang & Jesus Hernandez
Date: 3/8/17
This lab consisted of finding the distance it took for an elephant riding frictionless roller skates to stop. The elephant rode down a hill and rolled on a flat surface for a certain amount of time. Attached to the elephant was a rocket that provided a force in the direction opposite of the elephant's motion; this helped stop the elephant.
This problem could be done using calculus. Given to us were the equations for the mass of the elephant and the elephant's acceleration. The acceleration function could be integrated to find the velocity function, and the velocity function could be integrated to calculate the position function. Setting the velocity function equal to zero in order to find the time it took for the elephant to stop could help. This time, t, could be used in the position function so that we can calculate the distance it took for the elephant to stop. When functions are easy to integrate, problems like these are easy to solve. However, the acceleration functions might not always be simple to integrate. In cases like those, it is useful to use a spreadsheet in order to calculate what we solved for numerically.
This image shows how the spreadsheet was used to calculate the information we want numerically. The approach here was to use a set of formulas that would provide information about the elephant's motion during each time interval.
This image shows that when t= 19.7 seconds, the elephant reached the farthest distance it was going to go. The value given in the spreadsheet agrees with the answers Professor Wolf derived analytically.
Sometimes it is not that difficult to calculate the stopping distance, or when an object stops with some given equations. One could use calculus to find the answers needed. However, it is somewhat difficult to do this when the integration process involves tedious work. Therefore, it's worth knowing that these same answers could be derived numerically.
Initially, my group struggled to develop the appropriate equations to put into the cells. If it weren't for the guidance provided to us by our instructor, our calculations would not have matched the analytic results.
Name: Ray Arellano
Lab Partners: David Hwang & Jesus Hernandez
Date: 3/8/17
This lab consisted of finding the distance it took for an elephant riding frictionless roller skates to stop. The elephant rode down a hill and rolled on a flat surface for a certain amount of time. Attached to the elephant was a rocket that provided a force in the direction opposite of the elephant's motion; this helped stop the elephant.
This problem could be done using calculus. Given to us were the equations for the mass of the elephant and the elephant's acceleration. The acceleration function could be integrated to find the velocity function, and the velocity function could be integrated to calculate the position function. Setting the velocity function equal to zero in order to find the time it took for the elephant to stop could help. This time, t, could be used in the position function so that we can calculate the distance it took for the elephant to stop. When functions are easy to integrate, problems like these are easy to solve. However, the acceleration functions might not always be simple to integrate. In cases like those, it is useful to use a spreadsheet in order to calculate what we solved for numerically.
This image shows how the spreadsheet was used to calculate the information we want numerically. The approach here was to use a set of formulas that would provide information about the elephant's motion during each time interval.
This image shows that when t= 19.7 seconds, the elephant reached the farthest distance it was going to go. The value given in the spreadsheet agrees with the answers Professor Wolf derived analytically.
Sometimes it is not that difficult to calculate the stopping distance, or when an object stops with some given equations. One could use calculus to find the answers needed. However, it is somewhat difficult to do this when the integration process involves tedious work. Therefore, it's worth knowing that these same answers could be derived numerically.
Initially, my group struggled to develop the appropriate equations to put into the cells. If it weren't for the guidance provided to us by our instructor, our calculations would not have matched the analytic results.
Tuesday, March 7, 2017
3-1-17: Finding "g" through free fall
1.Title: Finding "g" Using Free-Fall
Name: Ray Arellano
Lab Partners: David Hwang & Jesus Hernandez
Date: 3/1/17
2. In this experiment, we are going to use distance, time, and a velocity in order to calculate "g", the acceleration of free-falling objects on Earth due to gravity.
3. In order to measure "g" we had to measure the distance of an object experiencing free-fall. The apparatus we used allowed us to know when the object had reach certain distances. Compiling this information on Excel helped my group develop a Position Vs Time graph and a Velocity Vs Time graph. In the end, we took the derivative of the equation of our Velocity Vs Time graph in order to discover what our experimental value of "g" was.
4.
This is our Position vs Time graph. It displays where the object was as time progressed.
Above is our Velocity vs Time graph. The equation for such a graph could be obtained by taking the first derivative of the position function.
8. Based on the function "y = 961.71x + 66.551" (our velocity function in the above picture), we calculated "g" to be 9.6171 m/s^2 by taking the derivative of "y" with respect to "x". The absolute difference between 9.8 m/s^2 (the accepted value of "g") and our experimental "g" is -0.1829 m/s^2. Sources of error for this experiment include the interpretation of the marks on the strip of paper. My group assumed that only the darkest marks were the most meaningful marks; we believed that the other marks were a result of sparks coming to an end. Also, air resistance could have slowed down the object that was falling, causing its acceleration towards the ground to be smaller than the expected value of 9.8 m/s^2. Our measurements with the 2-meter stick could also have been flawed; the marks on the stick are small enough to make errors while reading it. If this was so, the velocity of the object could have been faster or slower at certain times. When taking into account all of these sources of error, it becomes understandable why our experimental value of "g" does not match the accepted value of "g".
Name: Ray Arellano
Lab Partners: David Hwang & Jesus Hernandez
Date: 3/1/17
2. In this experiment, we are going to use distance, time, and a velocity in order to calculate "g", the acceleration of free-falling objects on Earth due to gravity.
3. In order to measure "g" we had to measure the distance of an object experiencing free-fall. The apparatus we used allowed us to know when the object had reach certain distances. Compiling this information on Excel helped my group develop a Position Vs Time graph and a Velocity Vs Time graph. In the end, we took the derivative of the equation of our Velocity Vs Time graph in order to discover what our experimental value of "g" was.
4.
This image shows the apparatus used for this experiment. This machine holds an object that is ready to fall and has a strip of paper stretched along the path of the object's descent. Sparks are generated every 1/60th of a second; these sparks mark the paper and allow us to understand where and how far the object traveled for a certain amount of time.
This is the strip of paper that was marked by the sparks.Next to it was a 2-meter stick that we used to collect measurements; we took the first mark on the paper to be the initial position and measured the distances between each mark that followed.
5.The excel sheet we used to hold our data was saved in an incorrect format and cannot be displayed. However, I personally took pictures of the graphs that correspond to our data 6.
This is our Position vs Time graph. It displays where the object was as time progressed.
Above is our Velocity vs Time graph. The equation for such a graph could be obtained by taking the first derivative of the position function.
8. Based on the function "y = 961.71x + 66.551" (our velocity function in the above picture), we calculated "g" to be 9.6171 m/s^2 by taking the derivative of "y" with respect to "x". The absolute difference between 9.8 m/s^2 (the accepted value of "g") and our experimental "g" is -0.1829 m/s^2. Sources of error for this experiment include the interpretation of the marks on the strip of paper. My group assumed that only the darkest marks were the most meaningful marks; we believed that the other marks were a result of sparks coming to an end. Also, air resistance could have slowed down the object that was falling, causing its acceleration towards the ground to be smaller than the expected value of 9.8 m/s^2. Our measurements with the 2-meter stick could also have been flawed; the marks on the stick are small enough to make errors while reading it. If this was so, the velocity of the object could have been faster or slower at certain times. When taking into account all of these sources of error, it becomes understandable why our experimental value of "g" does not match the accepted value of "g".
Sunday, March 5, 2017
27-Feb-2017: Calculating an unknown mass added to an inertial pendulum
The purpose of this lab was to determine the mass of objects placed on an inertial pendulum. In order to achieve this we used the model "T = A(m +Mtray)^n". However, this model is of little value to us without taking data because the only thing we can find using the inertial pendulum is the period, T. This model can be manipulated to take on a form similar to "y = mx + b" by setting it in the form"lnT = nln(m+Mtray) + lnA", which will allow us to make a graph that will help identify values for "A", the y-intercept of the lnT graph and "n", the slope of the lnT graph. Identifying these values is useful to us because doing so will assist us in finding the mass of any object placed on the inertial pendulum (we will have an equation with variables whose values we know; we would only be solving for "m", the mass added to the inertial pendulum).
This image shows the inertial pendulum with mass added to the end. The blue strip of tape passes through a photogate which measures the period of oscillation of the inertial pendulum. Each period corresponds to the specific mass added to the pendulum.
Starting the process of creating the "lnT = nln(m +Mtray) + lnA" graph began with collecting data. The image above shows the resulting period, T, of various masses added to the inertial pendulum. This data was developed into a graph that would eventually be altered to display "lnT" on the y-axis and "ln(m + Mtray)" on the x-axis.
This graph, and the following graphs as well, represent the model "lnT = nln(m + Mtray) + lnA". These graphs allow us to derive "n", the slope th of graph, and "A" the y-intercept of the graph as well. However, in order to obtain a straight line, we had to guess the mass of the tray, Mtray. In this case, a mass of 280g was assigned to be the mass of the tray. Doing this resulted in a correlation of 0.9995, which is a good indicator that our line is straight.
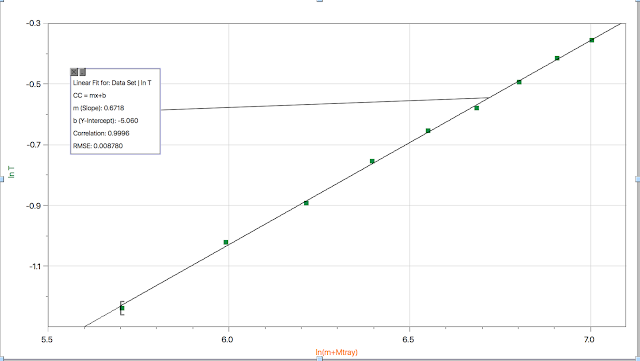
This graph produced the highest correlation, 0.9996. The mass assigned to the tray was 300g.
Lastly, this graph produced the lowest correlation, 0.9994. The mass assigned to the tray was 340g. At this point, each graph yields information that we can use in the model "T = A|(m + Mtray)^n"; these graphs provide us with "n", "A", and Mtray.
Now that we can apply these variables (with known values) into the aforementioned model, it was our job to place the objects with unknown masses (an eraser and a wallet) on the tray of the inertial pendulum and discover what their period of oscillation was. While we actually weighed the objects to know what their masses are, the purpose of finding the period of their oscillations was so that we could use it in the model "T = A(m + Mtray)^n". We now have what we did not have at the start of the lab; we have four known variables and one unknown variable. Solving for "m", the mass added to the tray, becomes a question of math.
Using the information we derived from the "lnT" models and period of oscillation for each unknown mass, we were able to solve the "T" model for "m" and compare the calculated mass to the actual mass of the unknown objects.The values for Mtray, "n", and "A" were applied to each unknown mass and its corresponding period. The result: six measurements for the calculated mass of the unknown masses (which we knew). The calculated mass for each were close to the actual mass of the objects for each time we solved the equations.
Although we tried our best to be as precise as possible and follow the directions as best as we could, there were some things that we could have done better. For one, we were not sure exactly where to place the masses/objects on the tray of the inertial pendulum. The masses/objects swayed side-to-side as the inertial pendulum moved.
This image shows the inertial pendulum with mass added to the end. The blue strip of tape passes through a photogate which measures the period of oscillation of the inertial pendulum. Each period corresponds to the specific mass added to the pendulum.
Starting the process of creating the "lnT = nln(m +Mtray) + lnA" graph began with collecting data. The image above shows the resulting period, T, of various masses added to the inertial pendulum. This data was developed into a graph that would eventually be altered to display "lnT" on the y-axis and "ln(m + Mtray)" on the x-axis.
This graph, and the following graphs as well, represent the model "lnT = nln(m + Mtray) + lnA". These graphs allow us to derive "n", the slope th of graph, and "A" the y-intercept of the graph as well. However, in order to obtain a straight line, we had to guess the mass of the tray, Mtray. In this case, a mass of 280g was assigned to be the mass of the tray. Doing this resulted in a correlation of 0.9995, which is a good indicator that our line is straight.
This graph produced the highest correlation, 0.9996. The mass assigned to the tray was 300g.
Lastly, this graph produced the lowest correlation, 0.9994. The mass assigned to the tray was 340g. At this point, each graph yields information that we can use in the model "T = A|(m + Mtray)^n"; these graphs provide us with "n", "A", and Mtray.
Now that we can apply these variables (with known values) into the aforementioned model, it was our job to place the objects with unknown masses (an eraser and a wallet) on the tray of the inertial pendulum and discover what their period of oscillation was. While we actually weighed the objects to know what their masses are, the purpose of finding the period of their oscillations was so that we could use it in the model "T = A(m + Mtray)^n". We now have what we did not have at the start of the lab; we have four known variables and one unknown variable. Solving for "m", the mass added to the tray, becomes a question of math.
Using the information we derived from the "lnT" models and period of oscillation for each unknown mass, we were able to solve the "T" model for "m" and compare the calculated mass to the actual mass of the unknown objects.The values for Mtray, "n", and "A" were applied to each unknown mass and its corresponding period. The result: six measurements for the calculated mass of the unknown masses (which we knew). The calculated mass for each were close to the actual mass of the objects for each time we solved the equations.
Although we tried our best to be as precise as possible and follow the directions as best as we could, there were some things that we could have done better. For one, we were not sure exactly where to place the masses/objects on the tray of the inertial pendulum. The masses/objects swayed side-to-side as the inertial pendulum moved.
Subscribe to:
Comments (Atom)